An Exception to a Keynesian Rule?
Paul Krugman warns against “caricaturing” Keynesian economics, and in particular the General Theory (GT), Keynes’s best known work. One caricature heard from time to time is that the book is not mathematically tractable. The caricature also claims that no one has succeeded in fitting such a contradictory and confusing bunch of arguments into a clear, mathematically coherent model. Okay, in the spirit of a concession to these macro skeptics, what follows is a schematic caricature of sorts that seems okay to me as a broad summary of the first 18 chapters or so of the book, from a classic book by Pasinetti. So for those who insist that (1) they need a preview in a very concise form or (2) that they will never have time for the lengthy and complicated GT, below is the aforementioned schema. It is only meant to show that one can in fact simplify this oft-misinterpreted work quite a bit using mathematical symbols and keep the gist of the first part of the story.
where the variables are defined as follows:
L = liquidity preference (psychological factors affecting long-term interest rates, especially expected future rate changes)
M-overbar = policy-determined money supply
I = nominal interest rate
E = expected profitability of investment projects, given economic conditions
C = consumption
I = investment
Y = total output
All arrows (→) show directions of causality, so that A→B means that knowing A allows us to determine B.
Finally, f(), ψ(), and φ() signify functions endowed with properties that allow one to use math to analyze the model.
(I have altered some of Pasinetti’s notation slightly.)
As Pasinetti points out, this causal schema is different from Krugman’s favored IS-LM model, and it does leave out much that is important, including changes in the numéraire (chapter 19) and long-run dynamics, which the formal argument left up in the air. In a footnote, Pasinetti says that the model is only a first approximation to Keynes’s theory, and that care should be taken with attempts to do exercises involving shifts in the curves. But while Pasinetti’s schema, and the simple model it represents, certainly succeeds in simplifying the GT, it is really not a caricature. The original version of the schema can be found in Growth and Distribution, by Luigi Pasinetti, chapter II, Cambridge University Press, a 1974 collection of generally lucid essays (publisher’s book site).
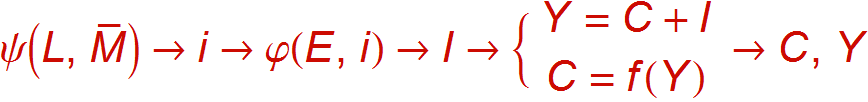



 ShareThis
ShareThis
How are the implications of this model different from IS-LM? They seem very similar to me.
Expectations are a big force in Keynes’s General Theory that is lacking in Hicks’s model. They enter into Pasinetti’s schema in the form of the variables L (for psychological aspects of the bond markets, which, by the way, asserted themselves in the bond markets last week) and E (for firms’ profitability expectations).
Also, Pasinetti argues that the gist of the Keynesian model is lost in IS-LM because certain arguments are added to the money-demand and investment functions. This aspect of IS-LM muddles key parts of Keynes’s message. The two changes are:
(1) the inclusion of the income variable Y in the money-demand function; and
(2) the inclusion of the interest rate i in the household-sector consumption function.
The first of these last two differences is not crucial in itself, according to Pasinetti’s argument, while the second is. It introduces a feedback effect from government policies that increase aggregate income to rising interest rates. This is the anti-Keynesian IS-LM crowding-out effect: fiscal stimulus leads to increases in aggregate income, which lead in turn to greater demand for money balances and thus to higher interest rates on government debt.
Thanks for the reply. It rings a bell because I remember looking through Alvin Hansen’s Guide to Keynes and seeing some discussion about this. He believed Keynes was mistaken in not including Y in liquidity preference. (full disclosure: Alvin Hansen was my great-grandfather – hence my possession of his book 🙂 )
To me, it seems reasonable that more income would mean a greater transactions demand for money. What’s your opinion on this?
Interesting comment. I don’t think that its unreasonable to include such an income variable, but probably not without including a lot of others and expecting to find a fairly unstable relationship. Of course, I am referring to an aggregate function here, since the topic is IS-LM and other similar models.
A large portion of money demand is for various financial transactions and uses, including trading of stocks, derivatives, and so on. Like the relationship between GDP growth and hiring, the link between GDP and the transactions demand for money has been affected by the expansion of the financial sector in recent decades. Then, there is the matter of constructing series that correct for institutional changes, such as changes in reserve requirements for bank accounts. Good measures of the stock of money are broad, and include large CDs, etc., since such assets are highly liquid (quickly convertible to spendable types of cash). Empirical studies show that estimated money demand functions, whether they include income or not, tend to be somewhat unstable, leading one to the conclusion that psychological factors and institutional changes are likely to be extremely potent. Among various psychological factors, Keynes of course emphasized changing bond-market views about future interest rates.